الرياضياتعلم مواضيعه مفاهيم مجردة والاصطلاحات الرياضية تدل على الكم، والعدد يدلّ على كمية المعدود والمقدار قابل للزيادة أو النقصان وعندما نستطيع قياس المقدار نطلق عليه اسم الكم. لذلك عرف بعض العلماء الرياضيات بأنه علم القياس. تعتبر الرياضيات لغة العلوم إذ إن هذه العلوم لا تكتمل إلا عندما نحول نتائجها إلى معادلات ونحول ثوابتها إلى خطوط بيانية.
تعرف الرياضيات بأنها دراسة القياس والحساب والهندسة. هذا بالإضافة إلى المفاهيم الحديثة نسبياً ومنها البنية، الفضاء أو الفراغ، والتغير والأبعاد. وبشكل عام قد يعرفها البعض على أنها دراسة البنى المجردة باستخدام المنطق والبراهين الرياضية والتدوين الرياضي. وبشكل أكثر عمومية، قد تعرف الرياضيات أيضاً على أنها دراسة الأعداد وأنماطها.
و لقد نشأت الرياضيات بقيام الإنسان بقياس ما يشاهده من ظواهر الطبيعة بناء على فطرة وخاصية في الإنسان ألا وهي اهتمامه بقياس كل ما حوله إلى جانب احتياجاته العملية فهكذا كان هناك ضرورة لقياس قسمة المقوتة (الطعام) بين أفراد العائلة وقياس الوقت والفصول والمحاصيل الزراعية تقسيم الأراضي وغنائم الحملات الحربية والمحاسبة للتمكن من الإتجار إلى جانب علم الملاحة بالنجوم في السفر والترحال للتجارة والاستكشاف والقياسات اللازمة لتشييد الأبنية والمدن.
و هكذا فإن البنى الرياضية التي يدرسها الرياضيون غالبا ما يعود أصلها إلى العلوم الطبيعية، وخاصة علم الطبيعة، ولكن الرياضيين يقومون بتعريف ودراسة بنى أخرى لأغراض رياضية بحتة، لأن هذه البنى قد توفر تعميما لحقول أخرى من الرياضيات مثلا، أو أن تكون عاملا مساعدا في حسابات معينة، وأخيرا فإن الرياضيين قد يدرسون حقولا معينة من الرياضيات لتحمسهم لها، معتبرين أن الرياضيات هي فن وليس علما تطبيقيا.
فللرياضيات دور بارز في علوم المادّة (أي الفيزياء والكيمياء) وعلم الأحياء (البيولوجيا)، فضلاً عن دوره المتميز في العلوم الإنسانية.
 مقال تفصيلي :تاريخ الرياضيات
كان الكُتاب البابليون منذ أكثر من 3000 عاما يمارسون كتابة الأعداد وحساب الفوائد ولاسيما في الأعمال التجارية ببابل. وكانت الأعداد والعمليات الحسابية تدون فوق ألواح الصلصال بقلم من البوص المدبب. ثم توضع في الفرن لتجف. وكانوا يعرفون الجمع والضرب والطرح والقسمة. ولم يكونوا يستخدمون فيها النظام العشري المتبع حاليا مما زادها صعوبة حيث كانوا يتبعون النظام الستيني الذي يتكون من 60 رمزا للدلالة علي الأعداد من 1-60. وطور قدماء المصريين هذا النظام في مسح الأراضي بعد كل فيضان لتقدير الضرائب. كما كانوا يتبعون النظام العشري وهو العد بالآحاد والعشرات والمئات. لكنهم لم يعرفوا الصفر. لهذا كانوا يكتبون 600 بوضع 6 رموز يعبر كل رمز على 100.
مقال تفصيلي :تاريخ الرياضيات
كان الكُتاب البابليون منذ أكثر من 3000 عاما يمارسون كتابة الأعداد وحساب الفوائد ولاسيما في الأعمال التجارية ببابل. وكانت الأعداد والعمليات الحسابية تدون فوق ألواح الصلصال بقلم من البوص المدبب. ثم توضع في الفرن لتجف. وكانوا يعرفون الجمع والضرب والطرح والقسمة. ولم يكونوا يستخدمون فيها النظام العشري المتبع حاليا مما زادها صعوبة حيث كانوا يتبعون النظام الستيني الذي يتكون من 60 رمزا للدلالة علي الأعداد من 1-60. وطور قدماء المصريين هذا النظام في مسح الأراضي بعد كل فيضان لتقدير الضرائب. كما كانوا يتبعون النظام العشري وهو العد بالآحاد والعشرات والمئات. لكنهم لم يعرفوا الصفر. لهذا كانوا يكتبون 600 بوضع 6 رموز يعبر كل رمز على 100.

فاللغة الرياضية توفر للقوانين العلمية مزيدا من الدقة، ومن أبرز الأمثلة على دور الرياضيات في علوم المادة: قياس سرعة الرياح، وقياس قوة الزلازل، وقياس الضعط الجوي.
و كان علم الوراثة الأول من علوم الأحياء الذي اتبع علوم المادة في مسارها الرياضي، وقد طبقت قوانين "مندل" في المجال الحيواني بقصد تأصيل بعض الحيوانات وعزل خصائص معينة كاللون والشكل والقد. وركز العالم "مورغان" اختياراته على ذبابة الدروزوفيل فتوصل إلى تحديد الجينات الوراثية في كروموزومات نواة الخلية.
إن علماء البيولوجيا يعتبرون الإحصاءات الرياضية بمثابة استقصاء وشرح متميز للمعطيات الطبية. فإن قياس الثوابت البيلوجية والتسجيلات البيانية تشكل لغة شائعة جدا في علوم الأحياء. فتخطيط الدماغ، وتخطيط القلب، وقياس نسبة الزلال، وقياس ثابة السكر في الدم، وإحصاء عدد كريات الدم الحمراء والبيضاء، وقياس النمو والوزن كلها دلائل على دخول الرياضيات في علوم الأحياء.
بصفة عامة، يمكن للرياضيات أن يقسم إلى دراسة الكمية والبنية والفضاء والتغير (مما يعني الحسابيات والجبر والهندسة والتحليل).
جبر تجريدي – نظرية الأعداد – هندسة جبرية – نظرية المجموعات – مونويد – التحليل الرياضي – الطوبولوجيا – الجبر الخطي – نظرية المخططات – الجبر الشامل – نظرية الزمر – نظرية الترتيب – نظرية القياس
تعرف الرياضيات بأنها دراسة القياس والحساب والهندسة. هذا بالإضافة إلى المفاهيم الحديثة نسبياً ومنها البنية، الفضاء أو الفراغ، والتغير والأبعاد. وبشكل عام قد يعرفها البعض على أنها دراسة البنى المجردة باستخدام المنطق والبراهين الرياضية والتدوين الرياضي. وبشكل أكثر عمومية، قد تعرف الرياضيات أيضاً على أنها دراسة الأعداد وأنماطها.
و لقد نشأت الرياضيات بقيام الإنسان بقياس ما يشاهده من ظواهر الطبيعة بناء على فطرة وخاصية في الإنسان ألا وهي اهتمامه بقياس كل ما حوله إلى جانب احتياجاته العملية فهكذا كان هناك ضرورة لقياس قسمة المقوتة (الطعام) بين أفراد العائلة وقياس الوقت والفصول والمحاصيل الزراعية تقسيم الأراضي وغنائم الحملات الحربية والمحاسبة للتمكن من الإتجار إلى جانب علم الملاحة بالنجوم في السفر والترحال للتجارة والاستكشاف والقياسات اللازمة لتشييد الأبنية والمدن.
و هكذا فإن البنى الرياضية التي يدرسها الرياضيون غالبا ما يعود أصلها إلى العلوم الطبيعية، وخاصة علم الطبيعة، ولكن الرياضيين يقومون بتعريف ودراسة بنى أخرى لأغراض رياضية بحتة، لأن هذه البنى قد توفر تعميما لحقول أخرى من الرياضيات مثلا، أو أن تكون عاملا مساعدا في حسابات معينة، وأخيرا فإن الرياضيين قد يدرسون حقولا معينة من الرياضيات لتحمسهم لها، معتبرين أن الرياضيات هي فن وليس علما تطبيقيا.
فللرياضيات دور بارز في علوم المادّة (أي الفيزياء والكيمياء) وعلم الأحياء (البيولوجيا)، فضلاً عن دوره المتميز في العلوم الإنسانية.
محتويات |
[عدل] التاريخ

عالم الرياضيات الإغريقي فيثاغورس (حوالي 570 - حوالي 495 قبل الميلاد), ينسب إليه اكتشاف مبرهنة فيثاغورس.
[عدل] الرياضيات في علوم المادة
يبقى علم الفيزياء علما استقرائياً يعتمد في الأساس على مراقبة الظواهر الطبيعية واختبارها، ويستطيع في أقصى حده التعبير عن القوانين بلغة رياضية، فتكون الرياضيات في مجال علوم المادة لغة تعبير أكثر منها منهج اكتشاف، وهناك حالات عديدة كانت الرياضيات فيها أسلوب اكتشاف وبرهنة. فقد اكتشف الفلكي الفرنسي أوربان لوفيريي بالحسابات الرياضية مكان كوكب نبتون وبعده وكتلته قبل التحقق من وجوده الفعلي بالرصد وكان الفكر الرياضي عند "نيوتن" و"أينشتاين" سابقا إلى حد كبير على الاختبار، لكن يبقى الاختبار الضامن الأخير لصحة الاكتشافات في علوم المادة. أما فرضية تحويل الكون برمته إلى معادلة رياضية كبرى فيبقى حلماَ راود أذهان الفلاسفة والعلماء أمثال "ديكارت"، ولكن هذا الهدف الكبير يبقى مجرّد فرضيّة دونها صعوبات وتجاذبات علمية وفلسفية. فالعالم لا يستطيع استعمال المنهج الرياضي الاستنباطي في سائر العلوم إلا إذا سلب الواقع كثيرا من مضمونه.فاللغة الرياضية توفر للقوانين العلمية مزيدا من الدقة، ومن أبرز الأمثلة على دور الرياضيات في علوم المادة: قياس سرعة الرياح، وقياس قوة الزلازل، وقياس الضعط الجوي.
[عدل] الرياضيات في علوم الأحياء
إن نجاح المنهج الاختباري في علوم الأحياء هيأها لاستعمال اللغة الرياضية الرائجة جدا في مجال العلوم الفيزيوكيميائية. ولقد عارض بعض العلماء هذا داعيين إلى الحذر وعدم إقحام الرياضيات في علوم الأحياء قبل أن تمر هذه الأخيرة بشكل واف على مشرحة التحليل. فالعلم الذي يبلغ مبلغا كافيا من التطور هو الذي يمكن أن يطمح إلى هذه الدرجة العلمية الرياضية.و كان علم الوراثة الأول من علوم الأحياء الذي اتبع علوم المادة في مسارها الرياضي، وقد طبقت قوانين "مندل" في المجال الحيواني بقصد تأصيل بعض الحيوانات وعزل خصائص معينة كاللون والشكل والقد. وركز العالم "مورغان" اختياراته على ذبابة الدروزوفيل فتوصل إلى تحديد الجينات الوراثية في كروموزومات نواة الخلية.
إن علماء البيولوجيا يعتبرون الإحصاءات الرياضية بمثابة استقصاء وشرح متميز للمعطيات الطبية. فإن قياس الثوابت البيلوجية والتسجيلات البيانية تشكل لغة شائعة جدا في علوم الأحياء. فتخطيط الدماغ، وتخطيط القلب، وقياس نسبة الزلال، وقياس ثابة السكر في الدم، وإحصاء عدد كريات الدم الحمراء والبيضاء، وقياس النمو والوزن كلها دلائل على دخول الرياضيات في علوم الأحياء.
[عدل] مجالات الرياضيات
أدى الانتشار الواسع للمعرفة في العصر العلمي إلى التخصص حيث يوجد حاليا ما لا يقل عن المئات من التخصصات في الرياضيات، إذ يحتل تصنيف مواضيع الرياضيات ستا وأربعين صفحة.[عدل] أسس وفلسفة الرياضيات
[عدل] الرياضيات البحتة
قد تقسم الرياضيات إلى فروع حسب موضوع الدراسة الأساسي.[عدل] الكمية
 | 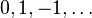 |  | |
| أعداد طبيعية | أعداد صحيحة | أعداد كسرية | |
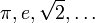 |  | ||
| أعداد حقيقية | أعداد مركبة أو عقدية |
- عدد – عدد طبيعي – عدد صحيح – عدد كسري – عدد حقيقي – عدد عقدي – عدد فوق عقدي – كواتيرنيون – اوكتونيون – سيدينيون – عدد فوق حقيقي – عدد حقيقي فائق – عدد ترتيبي – عدد كمي – عدد بي – متوالية صحيحة – ثابت رياضي – أسماء الأعداد – اللانهاية – الأساس (رياضيات)
[عدل] البنية
انظر إلى بنية رياضية.جبر تجريدي – نظرية الأعداد – هندسة جبرية – نظرية المجموعات – مونويد – التحليل الرياضي – الطوبولوجيا – الجبر الخطي – نظرية المخططات – الجبر الشامل – نظرية الزمر – نظرية الترتيب – نظرية القياس
[عدل] الفضاء
قد يسمى الفضاء أيضا فراغا.| طوبولوجيا | هندسة رياضية | |
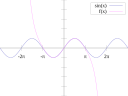 | ||
| هندسة تفاضلية | علم المثلثات | |
| هندسة كسيرية |
- طوبولوجيا – هندسة رياضية – علم المثلثات – هندسة جبرية – هندسة تفاضلية – طبولوجيا تفاضلية – طوبولوجيا جبرية – جبر خطي – هندسة كسيرية
[عدل] التغير
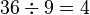 | ||
| حساب | تكامل | |
| تكامل شعاعي | ||
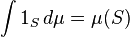 |  | |
| تحليل رياضي | معادلات تفاضلية | |
| جمل متحركة (ديناميكية) | نظرية الشواش |













ليست هناك تعليقات:
إرسال تعليق